Week 5: Estimation & Testing

Model Estimation and Testing

Week Learning Objectives

By the end of this module, you will be able to

• Describe, conceptually, what likelihood function and maximum likelihood estimation are
• Describe the differences between maximum likelihood and restricted maximum likelihood
• Conduct statistical tests for fixed effects, and use the small-sample correction when needed
• Use the likelihood ratio test to test random slopes
• Estimate multilevel models with the Bayesian/Markov Chain Monte Carlo estimator in the brms package

Task List

1. Review the resources (lecture videos and slides)
2. Complete the assigned readings
   • Snijders & Bosker ch 4.7, 6, 12.1, 12.2
3. Attend the Tuesday session and participate in the class exercise
4. (Optional) Fill out the early/mid-semester feedback survey on Blackboard

Lecture

Slides

PDF version

Estimation Methods

Overview

Estimation methods

Check your learning

The values you obtained from MLM software (e.g., lme4) are

Parameter values
Sample estimates

Likelihood function

Check your learning

In statistics, likelihood is the probability of

getting the sample data, for a given parameter value
the parameter being a certain value, for a given data set
the hypothesis being correct, for a given data set

Check your learning

Which of the following is possible as a value for log-likelihood?

10,300
-10,300
0.5

Estimation methods for MLM

Check your learning

The deviance is

2 x likelihood
2 x log-likelihood
-2 x log-likelihood

Testing

Likelihood ratio test (LRT) for fixed effects

The LRT has been used widely across many statistical methods, so it’s helpful to get familiar with doing it by hand (as it may not be available in all software in all procedures).

Check your learning

	Model 1	Model 2
(Intercept)	12.650	12.662
	(0.148)	(0.148)
meanses	5.863	3.674
	(0.359)	(0.375)
ses		2.191
		(0.109)
SD (Intercept id)	1.610	1.627
SD (Observations)	6.258	6.084
Num.Obs.	7185	7185
R2 Marg.	0.123	0.167
R2 Cond.	0.178	0.223
AIC	46969.3	46578.6
BIC	46996.8	46613.0
ICC	0.06	0.07
RMSE	6.21	6.03

Using R and the pchisq() function, what are the ${\chi }^2$ (or X2) test statistic and the $p$ value for the fixed effect coefficient for ses?

X2 = 395.3, df = 1, p < .001
X2 = 198, df = 1, p < .001
F = 20.1, df = 1, p < .001

$F$ test with small-sample correction

Check your learning

From the results below, what are the test statistic and the $p$ value for the fixed effect coefficient for meanses?

ABCDEFGHIJ0123456789

	Sum Sq <dbl>	Mean Sq <dbl>	NumDF <int>	DenDF <dbl>
meanses	324.3935	324.3935	1	15.5060
ses	1874.3379	1874.3379	1	669.0317

2 rows | 1-5 of 7 columns

<form name="form_38879" onsubmit="return validate_form_38879()" method="post"><input type="radio" name="answer_38879" id="38879_1" value="F(1) = 57.53, p < .001"><label for="1">F(1) = 57.53, p < .001</label><br><input type="radio" name="answer_38879" id="38879_2" value="X2 = 324.39, df = 15.51, p = .006"><label for="2">X2 = 324.39, df = 15.51, p = .006</label><br><input type="radio" name="answer_38879" id="38879_3" value="F(1, 15.51) = 9.96, p = .006"><label for="3">F(1, 15.51) = 9.96, p = .006</label><br><input type="submit" value="check"></form><p id="result_38879"></p><script> function validate_form_38879() {var x, text; var x = document.forms["form_38879"]["answer_38879"].value;if (x == "F(1, 15.51) = 9.96, p = .006"){text = 'Correct 👍';} else {text = 'That is not correct. Rewatch the video if needed';} document.getElementById('result_38879').innerHTML = text; return false;} </script>

For more information on REML and K-R, check out

• McNeish, D. (2017). Small sample methods for multilevel modeling: A colloquial elucidation of REML and the Kenward-Roger correction.

LRT for random slope variance

Check your learning

When testing whether the variance of a random slope term is zero, what needs to be done?

The p-value needs to be divided by 2, because the random slope variance can only be zero or positive
The p-value needs to be divided by 2 so that the results will be a two-tailed test
The p-value needs to be divided by 2, because it is a two degrees of freedom test

Multilevel bootstrap

Bayesian estimation

Check your learning

What does MCMC stand for?

Multiple-Chain Monte Carlo
Markov Chain Monte Carlo
Multilevel computational Monte Carlo

Check your learning

Which distribution is used to make statistical conclusions for Bayesian parameter estimation?

Prior distribution
Likelihood
Posterior distribution

Using brms

Bonus: Details of maximum likelihood

Check your learning: Using R, verify that, if $\mu =10$ and $\sigma =8$ for a normally distributed population, the probability (joint density) of getting students with scores of 23, 16, 5, 14, 7.

Check your learning: Using the principle of maximum likelihood, the best estimate for a parameter is one that

Check your learning

Using the principle of maximum likelihood, the best estimate for a parameter is one that

results in the least squared error
is the sample mean
maximizes the log-likelihood function

Think more

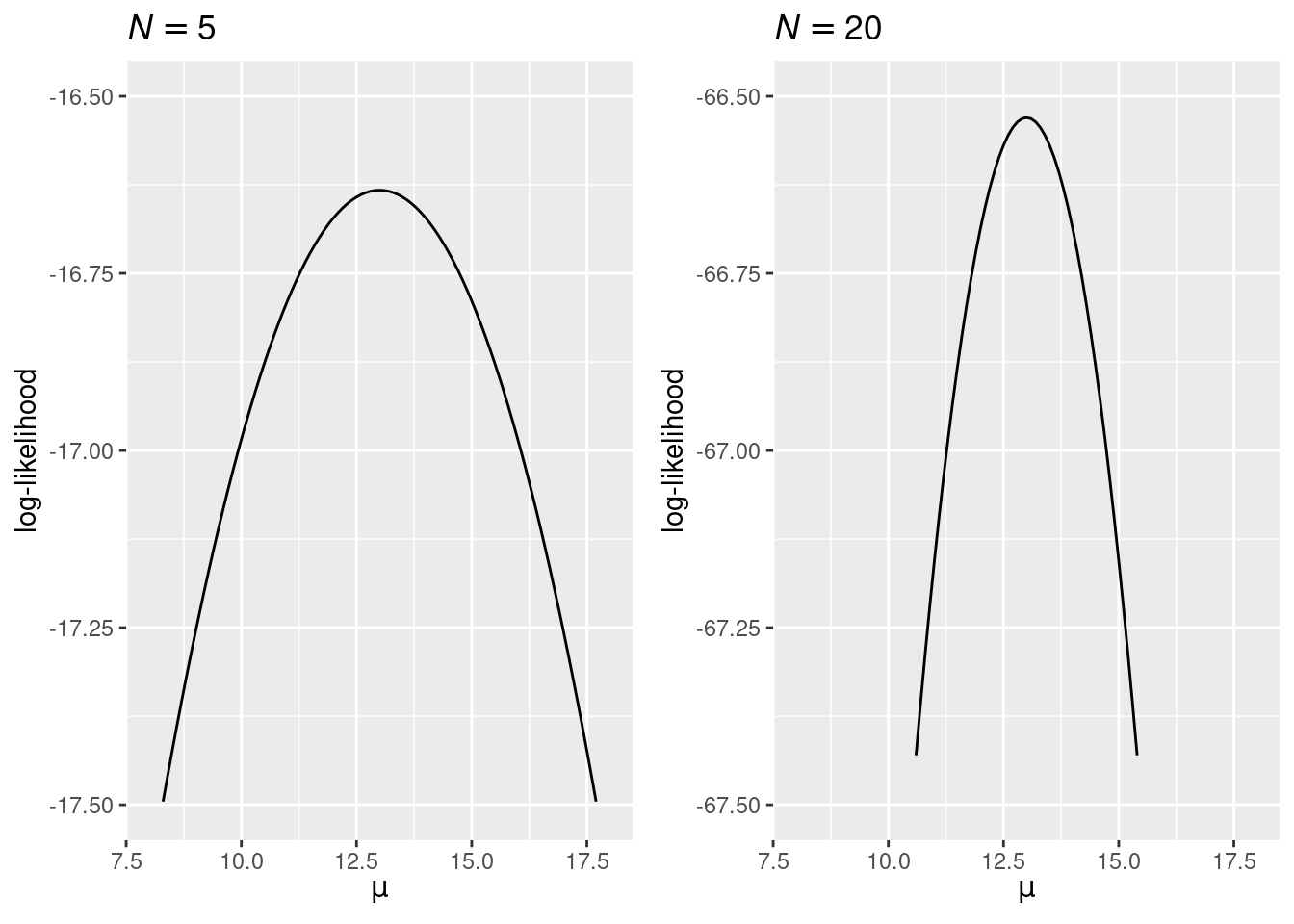
Because a probability is less than 1, the logarithm of it will be a negative number. By that logic, if the log-likelihood is -16.5 with $N=5$, what should it be with a larger sample size (e.g., $N=50$)?

more negative (e.g., -160.5)
unchanged (i.e., -16.5
more positive (e.g., -1.65)

More about maximum likelihood estimation

If $\sigma$ is not known, the maximum likelihood estimate is $$\hat{\sigma }=\sqrt{\frac{\sum _{i=1}^N(Y_i-\overline{X}{)}^2}{N}},$$ which uses $N$ in the denominator instead of $N-1$. Because of this, in small samples, maximum likelihood estimates tend to be biased, meaning that, on average, it tends to underestimate the population variance.

One useful property of maximum likelihood estimation is that the standard error can be approximated by the inverse of the curvature of the likelihood function at the peak. The two graphs below show that with a larger sample, the likelihood function has a higher curvature (i.e., steeper around the peak), which results in a smaller estimated standard error.