Model Estimation and Testing
PSYC 575
Mark Lai
University of Southern California
2020/09/01 (updated: 2022-09-17)
Week Learning Objectives
Describe, conceptually, what the likelihood function and maximum likelihood estimation are
Describe the differences between maximum likelihood and restricted maximum likelihood
Conduct statistical tests for fixed effects, and use the small-sample correction when needed
Use the likelihood ratio test to test random slopes
Estimate multilevel models with the Bayesian/Markov Chain Monte Carlo estimator in the
brmspackage
Estimation
Regression: OLS
MLM: Maximum likelihood, Bayesian
Why should I learn about estimation methods?
Why should I learn about estimation methods?
Understand software options
Why should I learn about estimation methods?
Understand software options
Know when to use better methods
Why should I learn about estimation methods?
Understand software options
Know when to use better methods
Needed for reporting
The most commonly used methods in MLM are
maximum likelihood (ML) and restricted maximum likelihood (REML)
># Linear mixed model fit by REML ['lmerMod']># Formula: Reaction ~ Days + (Days | Subject)># Data: sleepstudy># REML criterion at convergence: 1744># Random effects:># Groups Name Std.Dev. Corr># Subject (Intercept) 24.74 ># Days 5.92 0.07># Residual 25.59 ># Number of obs: 180, groups: Subject, 18># Fixed Effects:># (Intercept) Days ># 251.4 10.5Estimation Methods for MLM
For MLM
Find γs, τs, and σ that maximizes the likelihood function
ℓ(γ,τ,σ;y)=−12{log|V(τ,σ)|+(y−Xγ)⊤V−1(τ,σ)(y−Xγ)}+K
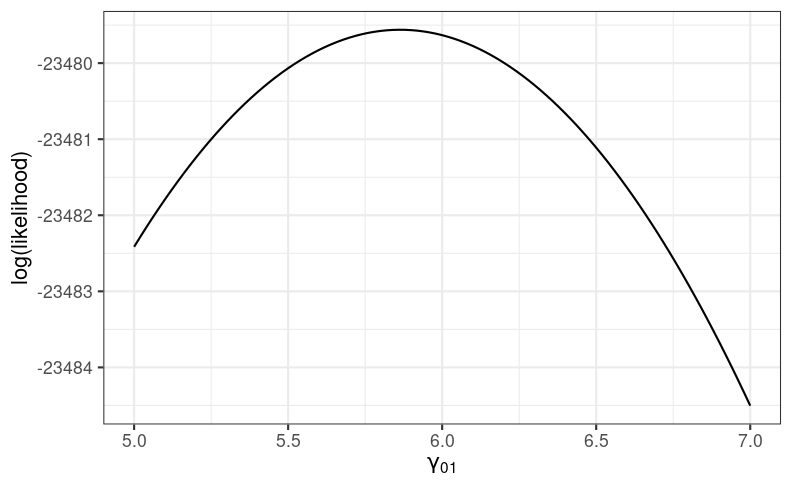
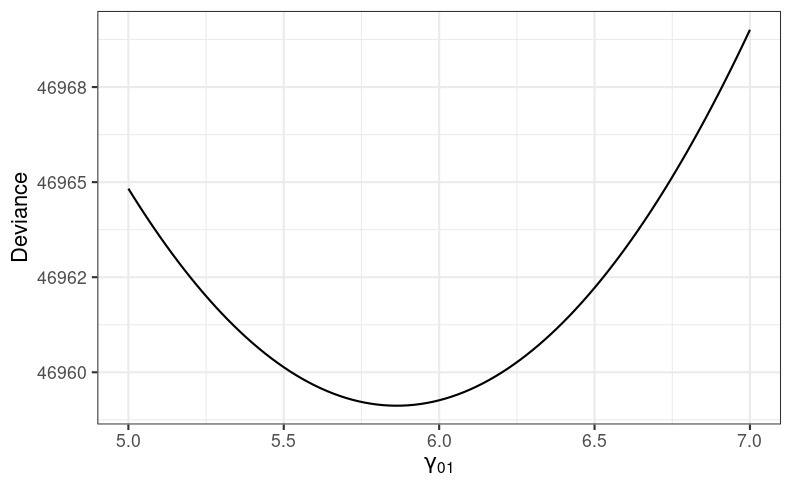
Here's the log-likelihood function for the coefficient of meanses (see code in the provided Rmd):
Numerical Algorithms
># iteration: 1># f(x) = 47022.519159># iteration: 2># f(x) = 47151.291766># iteration: 3># f(x) = 47039.480137># iteration: 4># f(x) = 46974.909593># iteration: 5># f(x) = 46990.872588># iteration: 6># f(x) = 46966.453125># iteration: 7># f(x) = 46961.719993># iteration: 8># f(x) = 46965.890703># iteration: 9># f(x) = 46961.367013># iteration: 10># f(x) = 46961.288830># iteration: 11># f(x) = 46961.298898># iteration: 12># f(x) = 46961.284848># iteration: 13># f(x) = 46961.285238># iteration: 14># f(x) = 46961.284845># iteration: 15># f(x) = 46961.284848># iteration: 16># f(x) = 46961.284845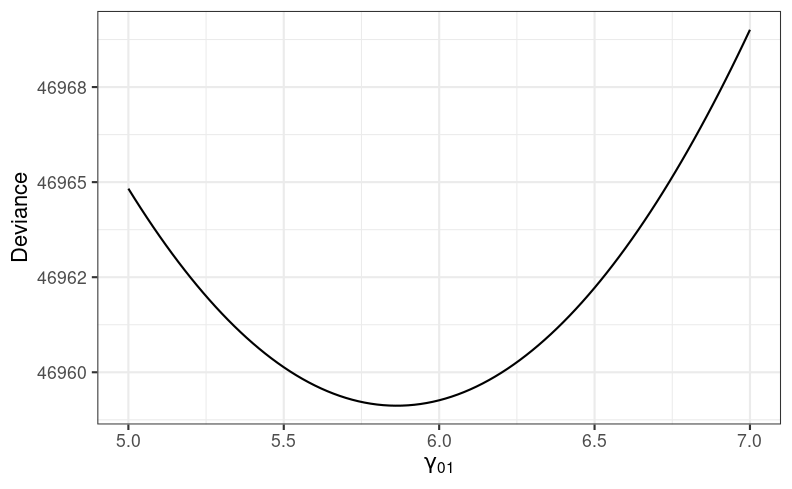
ML vs. REML
REML has corrected degrees of freedom for the variance component estimates (like dividing by N−1 instead of by N in estimating variance)
REML is generally preferred in smaller samples
The difference is small when the number of clusters is large
Technically speaking, REML only estimates the variance components1
[1] The fixed effects are integrated out and are not part of the likelihood function. They are solved in a second step, usually by the generalized least squares (GLS) method
160 Schools
| REML | ML | |
|---|---|---|
| (Intercept) | 12.649 | 12.650 |
| (0.149) | (0.148) | |
| meanses | 5.864 | 5.863 |
| (0.361) | (0.359) | |
| SD (Intercept id) | 1.624 | 1.610 |
| SD (Observations) | 6.258 | 6.258 |
| Num.Obs. | 7185 | 7185 |
| R2 Marg. | 0.123 | 0.123 |
| R2 Cond. | 0.179 | 0.178 |
| AIC | 46969.3 | 46969.3 |
| BIC | 46996.8 | 46996.8 |
| ICC | 0.1 | 0.1 |
| RMSE | 6.21 | 6.21 |
160 Schools
| REML | ML | |
|---|---|---|
| (Intercept) | 12.649 | 12.650 |
| (0.149) | (0.148) | |
| meanses | 5.864 | 5.863 |
| (0.361) | (0.359) | |
| SD (Intercept id) | 1.624 | 1.610 |
| SD (Observations) | 6.258 | 6.258 |
| Num.Obs. | 7185 | 7185 |
| R2 Marg. | 0.123 | 0.123 |
| R2 Cond. | 0.179 | 0.178 |
| AIC | 46969.3 | 46969.3 |
| BIC | 46996.8 | 46996.8 |
| ICC | 0.1 | 0.1 |
| RMSE | 6.21 | 6.21 |
16 Schools
| REML | ML | |
|---|---|---|
| (Intercept) | 12.809 | 12.808 |
| (0.504) | (0.471) | |
| meanses | 6.577 | 6.568 |
| (1.281) | (1.197) | |
| SD (Intercept id) | 1.726 | 1.581 |
| SD (Observations) | 5.944 | 5.944 |
| Num.Obs. | 686 | 686 |
| R2 Marg. | 0.145 | 0.146 |
| R2 Cond. | 0.211 | 0.203 |
| AIC | 4419.6 | 4419.7 |
| BIC | 4437.7 | 4437.8 |
| ICC | 0.1 | 0.1 |
| RMSE | 5.89 | 5.89 |
Other Estimation Methods
Generalized estimating equations (GEE)
- Robust to some misspecification and non-normality
- Maybe inefficient in small samples (i.e., with lower power)
- See Snijders & Bosker 12.2; the
geepackR package
Markov Chain Monte Carlo (MCMC)/Bayesian
- Researchers set prior distributions for the parameters
- Different from "empirical Bayes": Prior coming from the data
- Does not depend on normality of the sampling distributions
- More stable in small samples with the use of priors
- Can handle complex models
- See Snijders & Bosker 12.1
Testing
Fixed effects (γ)
- Usually, the likelihood-based CI/likelihood-ratio (LRT; χ2) test is sufficient
- Require ML (as fixed effects are not part of the likelihood function in REML)
- Small sample (10--50 clusters): Kenward-Roger approximation of degrees of freedom
- Non-normality: Residual bootstrap1
Random effects (τ)
- LRT (with p values divided by 2)
[1]: See van der Leeden et al. (2008) and Lai (2021)
Testing Fixed Effects
Likelihood Ratio (Deviance) Test
H0:γ=0
Likelihood Ratio (Deviance) Test
H0:γ=0
Likelihood ratio: L(γ=0)L(γ=^γ)
Deviance: −2×log(L(γ=0)L(γ=^γ))
= −2LL(γ=0)−[−2LL(γ=^γ)]
= Deviance∣γ=0−Deviance∣γ=^γ
ML (instead of REML) should be used
Example
...># Linear mixed model fit by maximum likelihood ['lmerMod']># Formula: mathach ~ (1 | id)># AIC BIC logLik deviance df.resid ># 47122 47142 -23558 47116 7182 ......># Linear mixed model fit by maximum likelihood ['lmerMod']># Formula: mathach ~ meanses + (1 | id)># AIC BIC logLik deviance df.resid ># 46967 46995 -23480 46959 7181 ...pchisq(47115.81 - 46959.11, df = 1, lower.tail = FALSE)># [1] 5.95e-36In lme4, you can also use
anova(m_lv2, ran_int) # Automatically use MLProblem of LRT in Small Samples
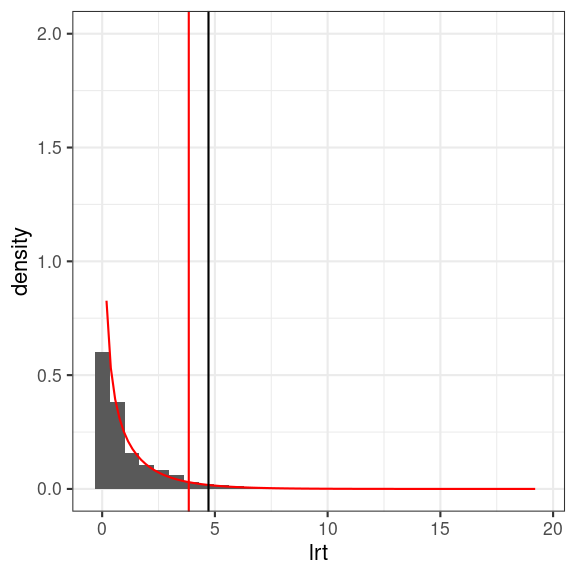
LRT assumes that the deviance under the null follows a χ2 distribution, which is not likely to hold in small samples
- Inflated Type I error rates
E.g., 16 Schools
- LRT critical value with α=.05: 3.84
- Simulation-based critical value: 4.72
Problem of LRT in Small Samples
LRT assumes that the deviance under the null follows a χ2 distribution, which is not likely to hold in small samples
- Inflated Type I error rates
E.g., 16 Schools
- LRT critical value with α=.05: 3.84
- Simulation-based critical value: 4.72
F Test With Small-Sample Correction
It is based on the Wald test (not the LRT):
- t=^γ/^se(^γ),
- Or equivalently, the F=t2 (for a one-parameter test)
The small-sample correction does two things:
- Adjust ^se(^γ) as it tends to be underestimated in small samples
- Determine the critical value based on an F distribution, with an approximate denominator degrees of freedom (ddf)
Kenward-Roger (1997) Correction
Generally performs well with < 50 clusters
# Waldanova(m_contextual, ddf = "lme4")># Analysis of Variance Table># npar Sum Sq Mean Sq F value># meanses 1 860 860 26.4># ses 1 1874 1874 57.5# K-R anova(m_contextual, ddf = "Kenward-Roger")># Type III Analysis of Variance Table with Kenward-Roger's method># Sum Sq Mean Sq NumDF DenDF F value Pr(>F) ># meanses 324 324 1 16 9.96 0.0063 ** ># ses 1874 1874 1 669 57.53 1.1e-13 ***># ---># Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1For meanses, the critical value (and the p value) is determined based on an F(1,15.51) distribution, which has a critical value of
qf(.95, df1 = 1, df2 = 15.51)># [1] 4.52Testing Random Effects
LRT for Random Slopes
Should you include random slopes?
Theoretically, yes, unless you're certain that the slopes are the same for every group
However, frequentist methods usually crash with more than two random slopes
- Test the random slopes one by one, and identify which one is needed
- Bayesian methods are more equipped for complex models
LRT for Random Slopes
Should you include random slopes?
Theoretically, yes, unless you're certain that the slopes are the same for every group
However, frequentist methods usually crash with more than two random slopes
- Test the random slopes one by one, and identify which one is needed
- Bayesian methods are more equipped for complex models
"One-tailed" LRT
LRT (χ2) is generally a two-tailed test. But for random slopes,
H0:τ1=0 is a one-tailed hypothesis
A quick solution is to divide the resulting p by 21
[1]: Originally proposed by Snijders & Bosker; tested in simulation by LaHuis & Ferguson (2009, https://doi.org/10.1177/1094428107308984)
Example: LRT for τ21
...># Formula: mathach ~ meanses + ses_cmc + (ses_cmc | id)># Data: hsball># REML criterion at convergence: 46558......># Formula: mathach ~ meanses + ses_cmc + (1 | id)># Data: hsball># REML criterion at convergence: 46569...Example: LRT for τ21
...># Formula: mathach ~ meanses + ses_cmc + (ses_cmc | id)># Data: hsball># REML criterion at convergence: 46558......># Formula: mathach ~ meanses + ses_cmc + (1 | id)># Data: hsball># REML criterion at convergence: 46569...G Matrix
[τ20τ01τ21]
[τ2000]
Example: LRT for τ21
...># Formula: mathach ~ meanses + ses_cmc + (ses_cmc | id)># Data: hsball># REML criterion at convergence: 46558......># Formula: mathach ~ meanses + ses_cmc + (1 | id)># Data: hsball># REML criterion at convergence: 46569...G Matrix
[τ20τ01τ21]
[τ2000]
pchisq(10.92681, df = 2, lower.tail = FALSE)># [1] 0.00424Need to divide by 2
Bayesian Estimation
Benefits
Better small sample properties
Less likely to have convergence issues
CIs available for any quantities (R2, predictions, etc)
Support complex models not possible with
lme4- E.g., 2+ random slopes
Is getting increasingly popular in recent research
Downsides
Computationally more intensive
- But dealing with convergence issues with ML/REML may end up taking more time
Need to learn some new terminologies
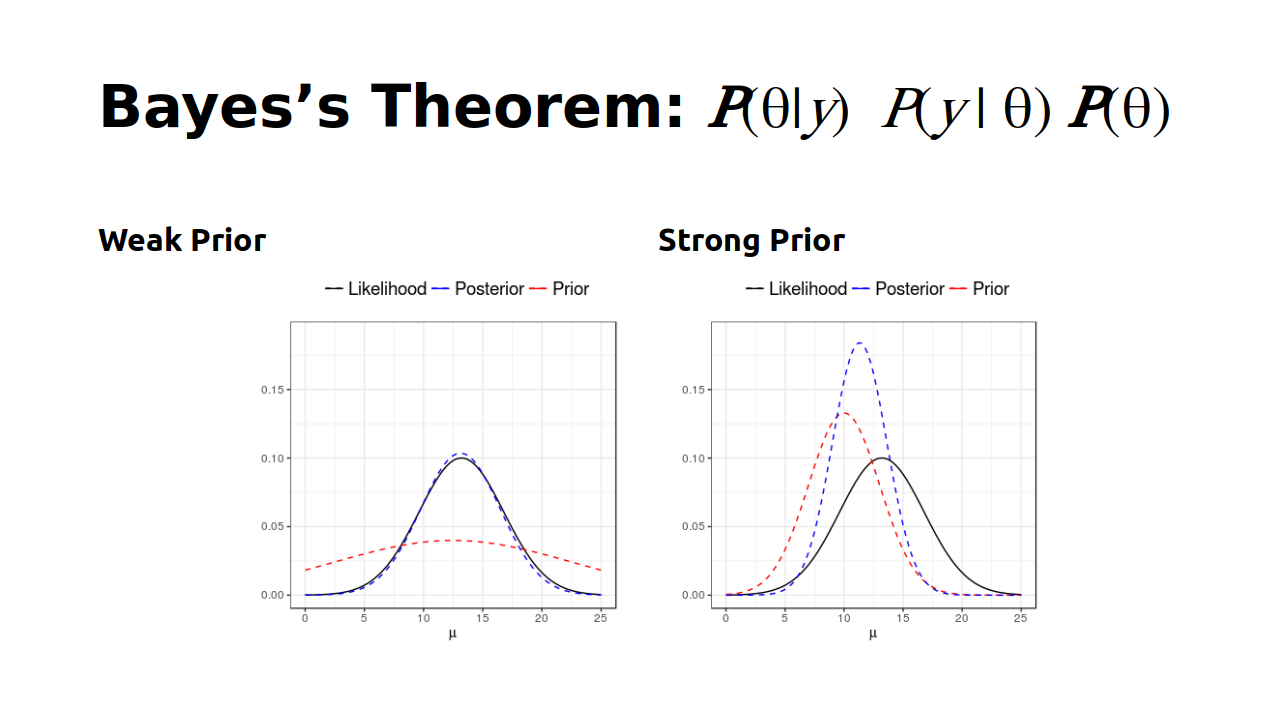
Bayes's Theorem
Posterior ∝ Likelihood × Prior
So, in addition to the likelihood function (as in ML/REML), we need prior information
Prior: Belief about a parameter before looking at the data
For this course, we use default priors set by the
brmspackage- Note that the default priors may change when software gets updated, so keep track of the package version when you run analyses
| MCMC | |
|---|---|
| b_Intercept | 12.647 |
| [12.348, 12.939] | |
| b_meanses | 5.854 |
| [5.141, 6.606] | |
| sd_id__Intercept | 1.633 |
| [1.386, 1.901] | |
| sigma | 6.258 |
| [6.159, 6.365] | |
| Num.Obs. | 7185 |
| R2 | 0.173 |
| R2 Adj. | 0.158 |
| R2 Marg. | 0.123 |
| ELPD | −23433.7 |
| ELPD s.e. | 49.7 |
| LOOIC | 46867.5 |
| LOOIC s.e. | 99.4 |
| WAIC | 46867.1 |
| RMSE | 6.21 |
| r2.adjusted.marginal | 0.116 |
Testing for Bayesian Estimation
A coefficient is statistically different from zero when the 95% CI does not contain zero.
Multilevel Bootstrap
A simulation-based approach to approximate the sampling distribution of fixed and random effects
- Useful for obtaining CIs
- Especially for statistics that are functions of fixed/random effects (e.g., R2)
Parametric, Residual, and Cases bootstrap
A simulation-based approach to approximate the sampling distribution of fixed and random effects
- Useful for obtaining CIs
- Especially for statistics that are functions of fixed/random effects (e.g., R2)
Parametric, Residual, and Cases bootstrap
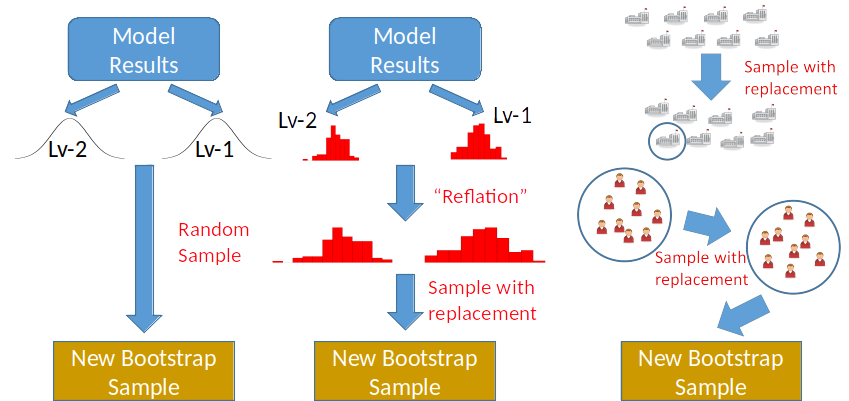
In my own work,1 the residual bootstrap was found to perform best, especially when data are not normally distributed and when the number of clusters is small
See R code for this week
Lai (2021, https://doi.org/10.1080/00273171.2020.1746902)
Bonus: More on Maximum Likelihood Estimation
What is Likelihood?
Let's say we want to estimate the population mean math achievement score (μ)
We need to make some assumptions:
Known SD: σ=8
The scores are normally distributed in the population
Learning the Parameter From the Sample
Assume that we have scores from 5 representative students
| Student | Score |
|---|---|
| 1 | 23 |
| 2 | 16 |
| 3 | 5 |
| 4 | 14 |
| 5 | 7 |
Likelihood
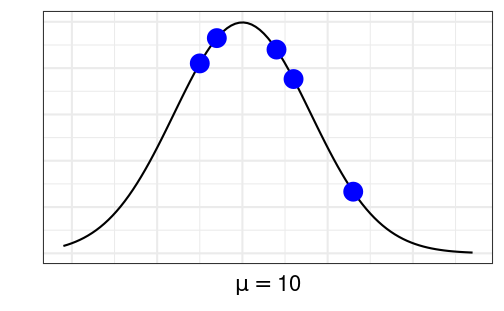
If we assume that μ=10, how likely will we get 5 students with these scores?
Likelihood
If we assume that μ=10, how likely will we get 5 students with these scores?

| Student | Score | `P(Yi=yi∣μ=10)` |
|---|---|---|
| 1 | 23 | 0.013 |
| 2 | 16 | 0.038 |
| 3 | 5 | 0.041 |
| 4 | 14 | 0.044 |
| 5 | 7 | 0.046 |
Multiplying them all together: P(Y1=23,Y2=16,Y3=5,Y4=14,Y5=7|μ=10) = Product of the probabilities =
># [1] 4.21e-08If μ=13
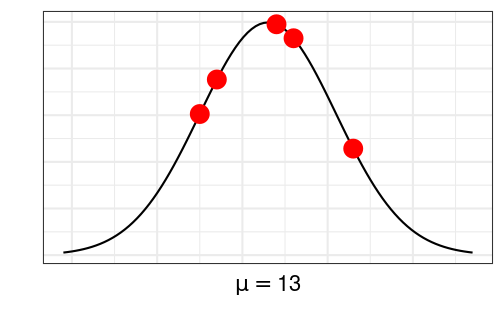
If μ=13

| Student | Score | `P(Yi=yi∣μ=13)` |
|---|---|---|
| 1 | 23 | 0.023 |
| 2 | 16 | 0.046 |
| 3 | 5 | 0.030 |
| 4 | 14 | 0.049 |
| 5 | 7 | 0.038 |
Multiplying them all together: P(Y1=23,Y2=16,Y3=5,Y4=14,Y5=7|μ=13) = Product of the probabilities =
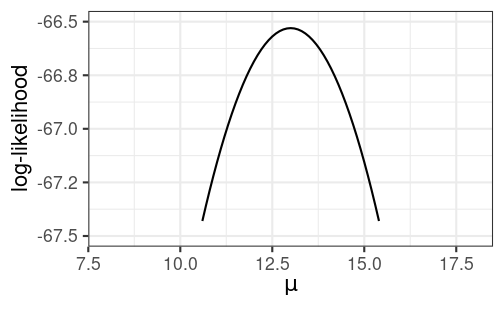
># [1] 5.98e-08Compute the likelihood for a range of μ values
Likelihood Function
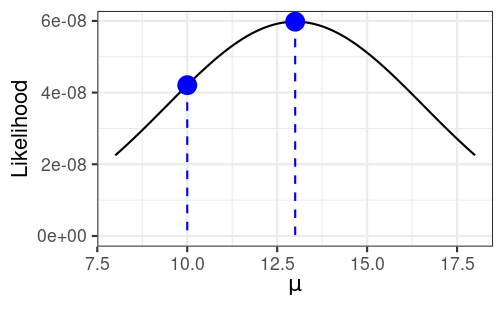
Compute the likelihood for a range of μ values
Likelihood Function

Log-Likelihood (LL) Function
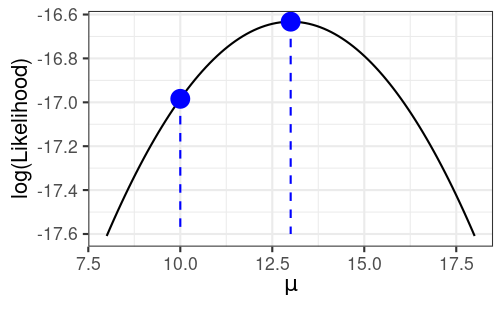
Maximum Likelihood
^μ=13 maximizes the (log) likelihood function
Maximum likelihood estimator (MLE)
Maximum Likelihood
^μ=13 maximizes the (log) likelihood function
Maximum likelihood estimator (MLE)
Estimating σ
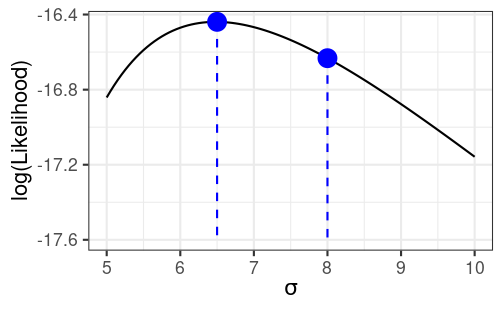
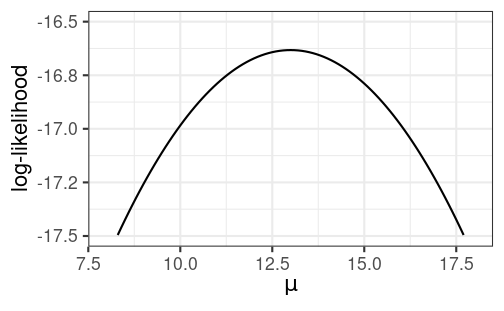
Curvature and Standard Errors
N=5
N=20