Multilevel Causal Inference
PSYC 575
Mark Lai
University of Southern California
2022/10/28 (updated: 2022-10-30)
Week Learning Objectives
Define causal effect from a causal inference framework
Describe what a confounder is using a directed acyclic graph (DAG)
Explain how randomized experiments control for confounders
Explain when and how statistical adjustment can potentially remove confounding
Explain how including cluster means can remove confounders at level 2
Reading
Rhoads & Li (2022) Chapter: Causal Inference in Multilevel Settings
Feller & Gelman (2015). Hierarchical Models for Causal Effects.
Causal Inference
When and how can we determine the causal effect of X on Y?
Causal Inference
When and how can we determine the causal effect of X on Y?
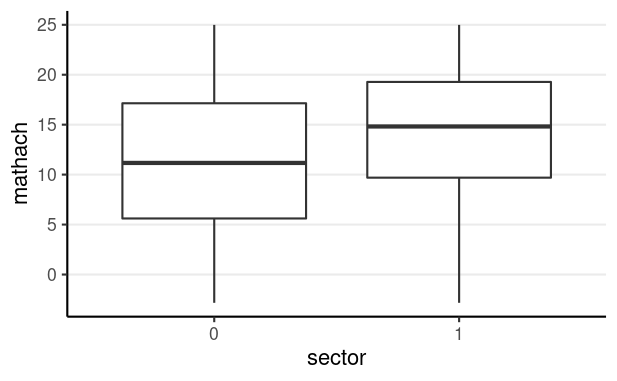
E.g., Sector on Achievement coefficient with HSB data
...># Formula: mathach ~ sector + (1 | id)># Data: hsball># ># Fixed effects:># Estimate Std. Error t value># (Intercept) 11.393 0.293 38.91># sector1 2.805 0.439 6.39...- The predicted difference in achievement between students in Catholic (
sector= 1) vs. public schools (sector= 0)
Causal Inference
When and how can we determine the causal effect of X on Y?
E.g., Sector on Achievement coefficient with HSB data
...># Formula: mathach ~ sector + (1 | id)># Data: hsball># ># Fixed effects:># Estimate Std. Error t value># (Intercept) 11.393 0.293 38.91># sector1 2.805 0.439 6.39...The predicted difference in achievement between students in Catholic (
sector= 1) vs. public schools (sector= 0)^Y∣X=1−^Y∣X=0
Causal Effect
What is the causal effect of sector on achievement?
Two interpretations:
Causal Effect
What is the causal effect of sector on achievement?
Two interpretations:
Predicting an intervention
- E.g., what would student i's achievement be if they move to a different type of school?
Causal Effect
What is the causal effect of sector on achievement?
Two interpretations:
Predicting an intervention
- E.g., what would student i's achievement be if they move to a different type of school?
Counterfactual
- E.g., what would student i's achievement have been if they had attended a different type of school?
Causal Inference Frameworks
Potential Outcome Framework (Holland, 19861; Rubin, 19742)
- Yij(1)−Yij(0)
Structural Causal Model (Pearl, 2000; 20093)
- Yij∣do(X=1)−Yij∣do(X=0)
[1] https://doi.org/10.1080/01621459.1986.10478354
[2] https://doi.org/10.1037/h0037350
[3] Pearl, J. (2009). Causality (2nd ed.).
Fundamental Problem of Causal Inference
| id | minority | female | ses | sector | mathach (sector = 0) | mathach (sector = 1) |
|---|---|---|---|---|---|---|
| 1224 | 0 | 1 | -1.528 | 0 | 5.88 | NA |
| 1224 | 0 | 1 | -0.588 | 0 | 19.71 | NA |
| 1224 | 0 | 0 | -0.528 | 0 | 20.35 | NA |
| 1224 | 0 | 0 | -0.668 | 0 | 8.78 | NA |
| 1224 | 0 | 0 | -0.158 | 0 | 17.90 | NA |
| 1224 | 0 | 0 | 0.022 | 0 | 4.58 | NA |
| 1308 | 0 | 0 | 0.422 | 1 | NA | 13.23 |
| 1308 | 0 | 0 | 0.562 | 1 | NA | 13.95 |
| 1308 | 1 | 0 | -0.058 | 1 | NA | 13.76 |
| 1308 | 0 | 0 | 0.952 | 1 | NA | 13.97 |
| 1308 | 0 | 0 | 0.622 | 1 | NA | 23.43 |
| 1308 | 0 | 0 | 0.832 | 1 | NA | 9.16 |
Maybe sector makes no difference . . .
| id | minority | female | ses | sector | mathach (sector = 0) | mathach (sector = 1) | causal effect |
|---|---|---|---|---|---|---|---|
| 1224 | 0 | 1 | -1.528 | 0 | 5.88 | 5.88 | 0 |
| 1224 | 0 | 1 | -0.588 | 0 | 19.71 | 19.71 | 0 |
| 1224 | 0 | 0 | -0.528 | 0 | 20.35 | 20.35 | 0 |
| 1224 | 0 | 0 | -0.668 | 0 | 8.78 | 8.78 | 0 |
| 1224 | 0 | 0 | -0.158 | 0 | 17.90 | 17.90 | 0 |
| 1224 | 0 | 0 | 0.022 | 0 | 4.58 | 4.58 | 0 |
| 1308 | 0 | 0 | 0.422 | 1 | 13.23 | 13.23 | 0 |
| 1308 | 0 | 0 | 0.562 | 1 | 13.95 | 13.95 | 0 |
| 1308 | 1 | 0 | -0.058 | 1 | 13.76 | 13.76 | 0 |
| 1308 | 0 | 0 | 0.952 | 1 | 13.97 | 13.97 | 0 |
| 1308 | 0 | 0 | 0.622 | 1 | 23.43 | 23.43 | 0 |
| 1308 | 0 | 0 | 0.832 | 1 | 9.16 | 9.16 | 0 |
Confounding
A confounder U is depicted in the following directed acyclic graph (DAG)
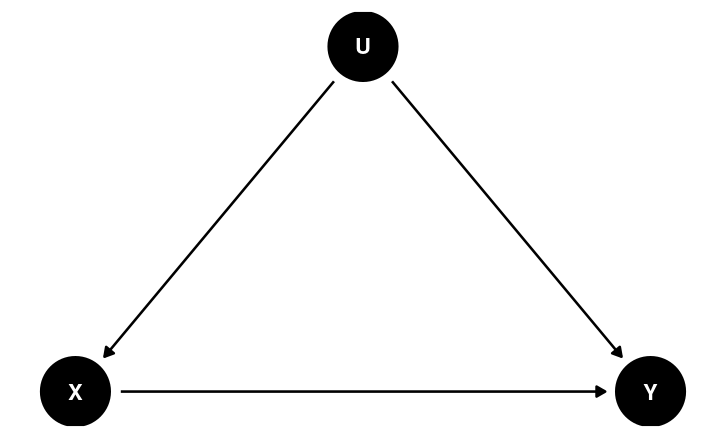
U biases the observed association between X and Y from the causal effect of X → Y
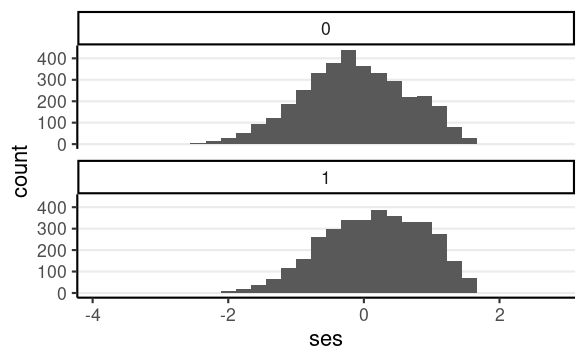
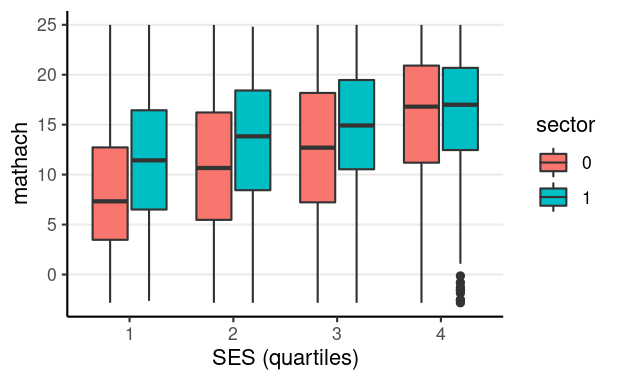
E.g., consider minority and ses as potential confounders
Proportion minority across sectors
| sector | minority |
|---|---|
| 0 | 0.253 |
| 1 | 0.297 |
Distribution of ses across sectors
Obtaining Causal Effects
Randomization
Unconfounding
Randomized Experiments
Why (and When) Does Randomized Experiment Work?
Remove all confounds (probabilistically)
- Intervention groups are different only by chance
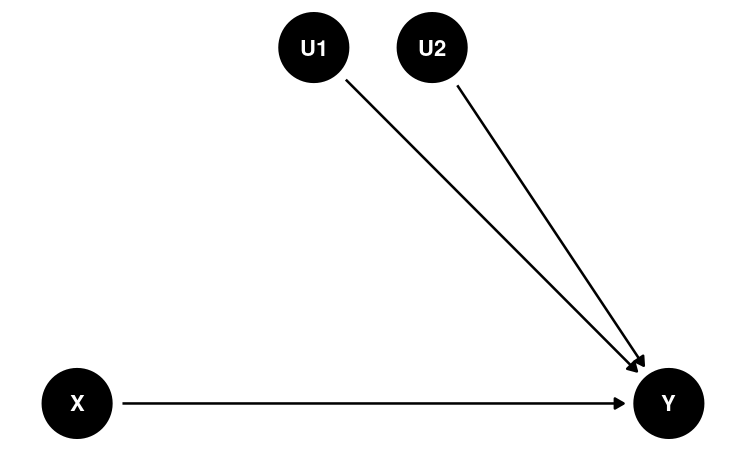
Average Treatment Effects
We still don't know the counterfactuals, but
- the distribution of Y(0) should be the same across the "intervention" groups (same for Y(1))
| id | minority | female | ses | sector | mathach (sector = 0) | mathach (sector = 1) |
|---|---|---|---|---|---|---|
| 1224 | 0 | 1 | -1.528 | 0 | 5.88 | NA |
| 1224 | 0 | 1 | -0.588 | 0 | 19.71 | NA |
| 1224 | 0 | 0 | -0.528 | 0 | 20.35 | NA |
| 1224 | 0 | 0 | -0.668 | 0 | 8.78 | NA |
| 1224 | 0 | 0 | -0.158 | 0 | 17.90 | NA |
| 1224 | 0 | 0 | 0.022 | 0 | 4.58 | NA |
| 1308 | 0 | 0 | 0.422 | 1 | NA | 13.23 |
| 1308 | 0 | 0 | 0.562 | 1 | NA | 13.95 |
| 1308 | 1 | 0 | -0.058 | 1 | NA | 13.76 |
| 1308 | 0 | 0 | 0.952 | 1 | NA | 13.97 |
| 1308 | 0 | 0 | 0.622 | 1 | NA | 23.43 |
| 1308 | 0 | 0 | 0.832 | 1 | NA | 9.16 |
Unconfounding: Statistical Adjustment
Why Do We Include Covariates?
Statistical control requires causal justification (Wysocki et al., 2022)1
One should adjust for
- Confounders
- Variables blocking confounding paths
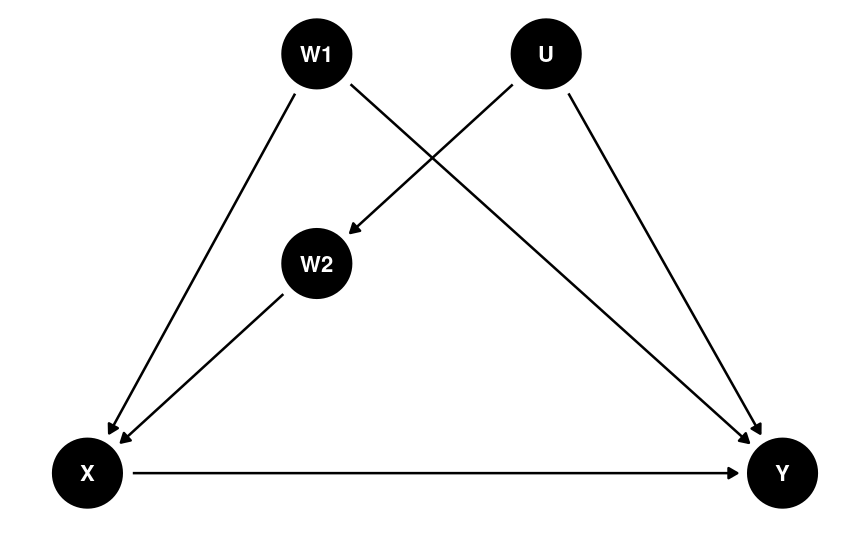
Statistical Adjustment/Control
Causal Inference With Observational Data
When all confounding paths between X and Y are successfully adjusted
Depends on causal assumptions
When some confounders are not measured, estimated effects are biased
When wrong variables are adjusted, estimated effects are biased
Confounder vs. Mediator
Do not blindly adjust/control for any variable!
- Mediator
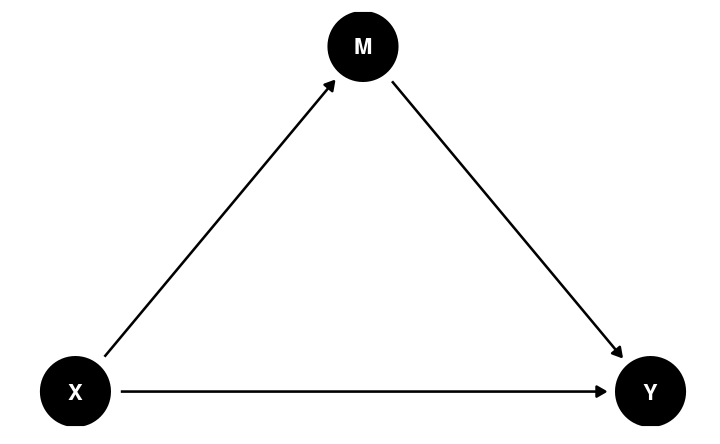
Example
Vaccine → Antibody → Symptom Severity
If adjust for Antibody, may falsely conclude vaccine has no effect
So, What to Adjust?
General rule of thumb: if interested in the total effect of X, do not adjust for variables that are potential consequences of X
Draw a DAG to identify variables on the confounding path
- Preferably, you have identified such variables in the planning stage, so that you can collect data on them
Using Multilevel Models for Causal Inference
Student Admissions at UC Berkeley (1973)
| Dept | App_Male | Admit_Male | Percent_Male | App_Female | Admit_Female | Percent_Female |
|---|---|---|---|---|---|---|
| A | 825 | 512 | 62.1 | 108 | 89 | 82.41 |
| B | 560 | 353 | 63.0 | 25 | 17 | 68.00 |
| C | 325 | 120 | 36.9 | 593 | 202 | 34.06 |
| D | 417 | 138 | 33.1 | 375 | 131 | 34.93 |
| E | 191 | 53 | 27.7 | 393 | 94 | 23.92 |
| F | 373 | 22 | 5.9 | 341 | 24 | 7.04 |
| Total | 2691 | 1198 | 44.5 | 1835 | 557 | 30.35 |
Without Adjustment
m1 <- glm(cbind(Admit, App - Admit) ~ Gender, data = berkeley_admit, family = binomial("logit"))summary(m1)...># Coefficients:># Estimate Std. Error z value Pr(>|z|) ># (Intercept) -0.2201 0.0388 -5.68 1.4e-08 ***># GenderFemale -0.6104 0.0639 -9.55 < 2e-16 ***># ---># Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1...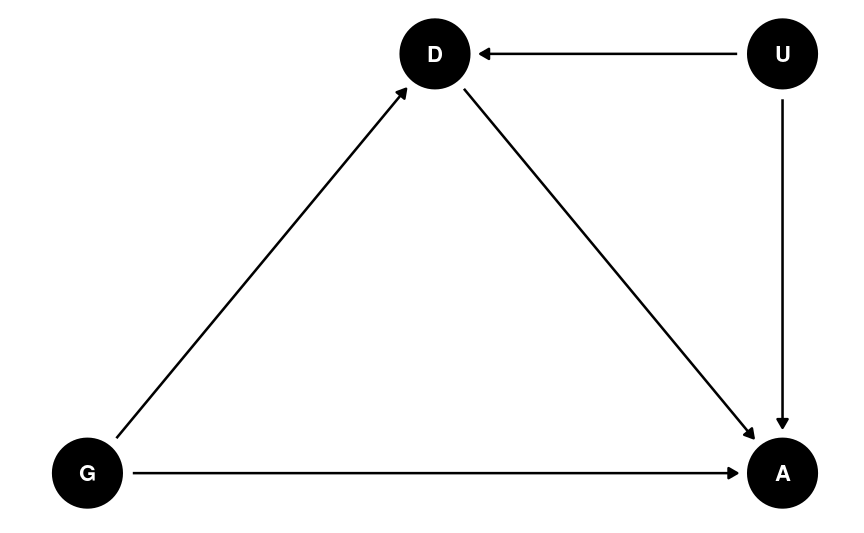
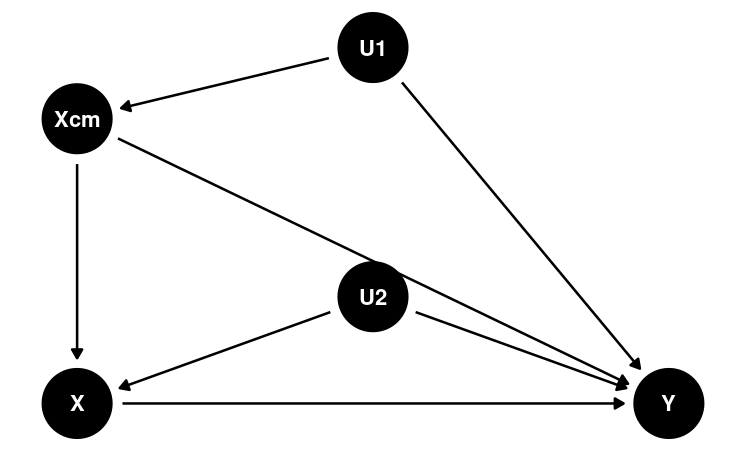
berkeley_admit <- berkeley_admit |> group_by(Dept) |> mutate(Gender_cm = App[2] / sum(App))m2 <- glmer(cbind(Admit, App - Admit) ~ Gender + Gender_cm + (Gender | Dept), data = berkeley_admit, family = binomial("logit"))summary(m2)...># Random effects:># Groups Name Variance Std.Dev. Corr ># Dept (Intercept) 0.743 0.862 ># GenderFemale 0.113 0.336 -0.14># Number of obs: 12, groups: Dept, 6># ># Fixed effects:># Estimate Std. Error z value Pr(>|z|)># (Intercept) 0.613 1.058 0.58 0.56># GenderFemale 0.169 0.172 0.98 0.33># Gender_cm -3.155 2.504 -1.26 0.21...The Role of Cluster Means
For level-1 X,
including cluster means of X adjusts for differences in X due to cluster-level confounders
Some Other Useful Tools
Mediation analysis
- Whether X has an effect on Y through M
- Check out the
mediationpackage
Propensity score
- Efficiently balancing multiple covariates
Instrumental variables (IVs)
- Variables inducing change in X, but should otherwise have no effects on Y
- E.g., the
plmpackage can perform IV estimation using the so-called Hausman-Taylor estimator
Causal discovery tools
- E.g.,
pcalgpackage
- E.g.,