Review of Regression Analysis
PSYC 575
Mark Lai
University of Southern California
2020/08/04 (updated: 2022-08-27)
Statistical Model
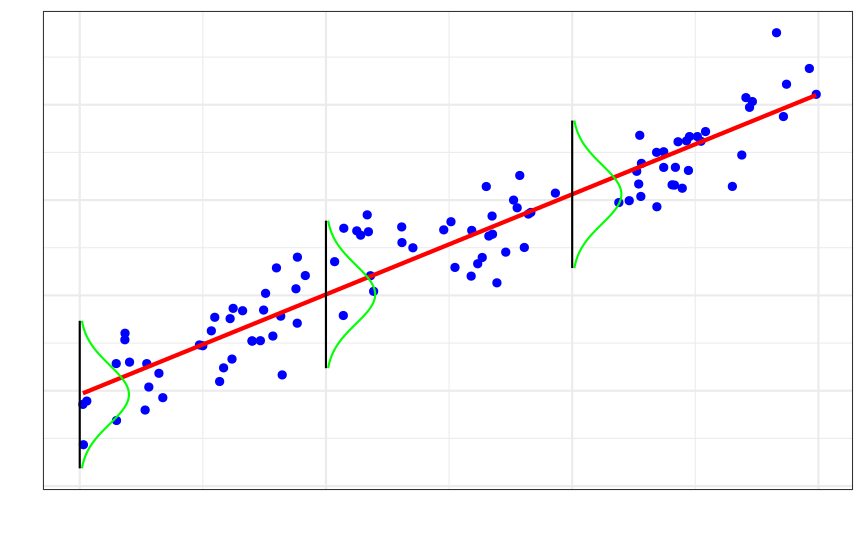
Statistical Model

A set of statistical assumptions describing how data are generated
- Deterministic/fixed component
Yi=β0+β1X1i+β2X2i+…
- Stochastic/random component
Yi=β0+β1X1i+β2X2i+…+ei ei∼N(0,σ)
- It's only a review, so I won't go deep.
- You may check out the sections in the book by Gelman et al.
- Model in OpenBoard
- Statistical notation
- Notation for normal distribution
- Important for MLM
Why Regression?
Why Regression?
MLM is an extension of multiple regression to deal with data from multiple levels
Learning Objectives
Refresh your memory on regression
Learning Objectives
Refresh your memory on regression
- Describe the statistical model
Learning Objectives
Refresh your memory on regression
Describe the statistical model
Write out the model equations
Learning Objectives
Refresh your memory on regression
Describe the statistical model
Write out the model equations
Simulate data based on a regression model
Learning Objectives
Refresh your memory on regression
Describe the statistical model
Write out the model equations
Simulate data based on a regression model
Plot interactions
R Demonstration
Transition to RStudio
- Data Import
- Explain the variables
Salary Data
From Cohen, Cohen, West & Aiken (2003)
Examine factors related to annual salary of faculty in a university department
Salary Data
From Cohen, Cohen, West & Aiken (2003)
Examine factors related to annual salary of faculty in a university department
- time = years after receiving degree
- pub = # of publications
- sex = gender (0 = male, 1 = female)
- citation = # of citations
- salary = annual salary
Data Exploration
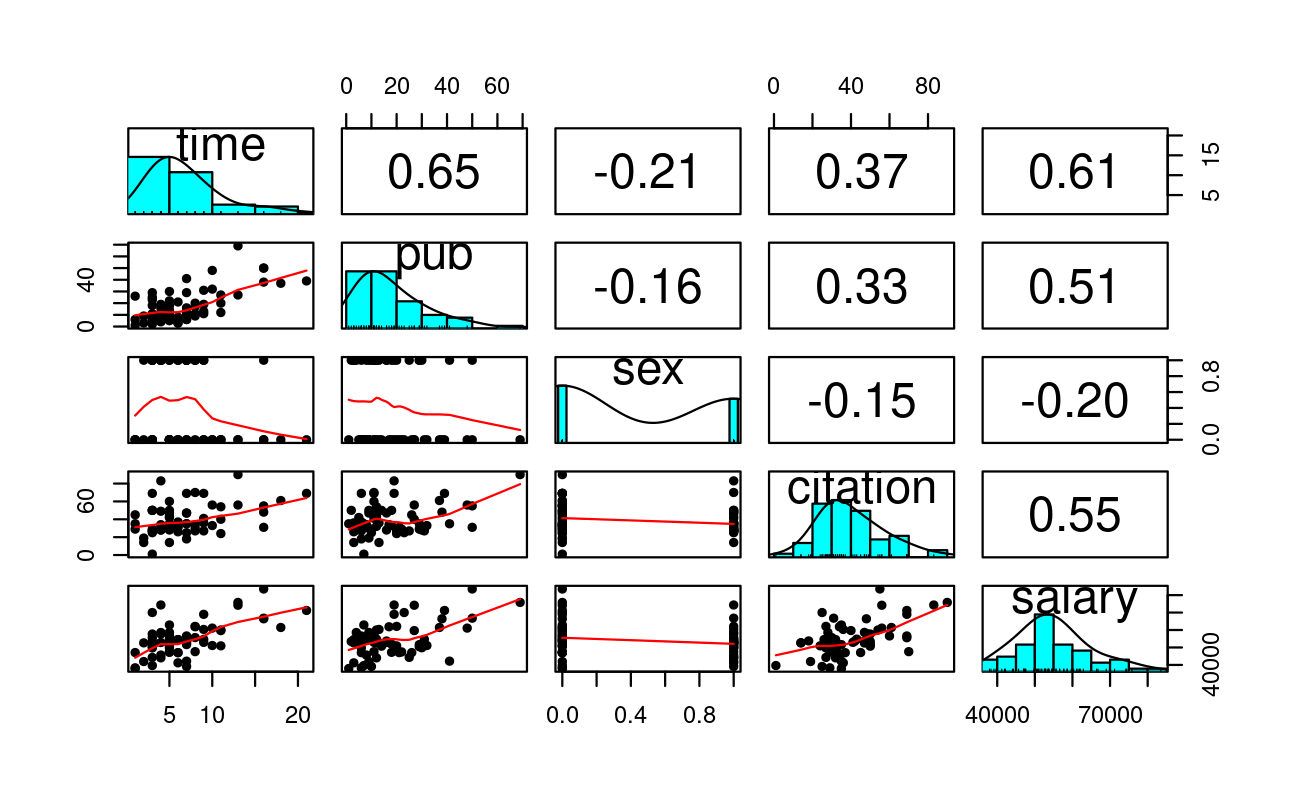
Explain what the x axis, y axis, diagonals are
Citation vs salary as an example
Data Exploration

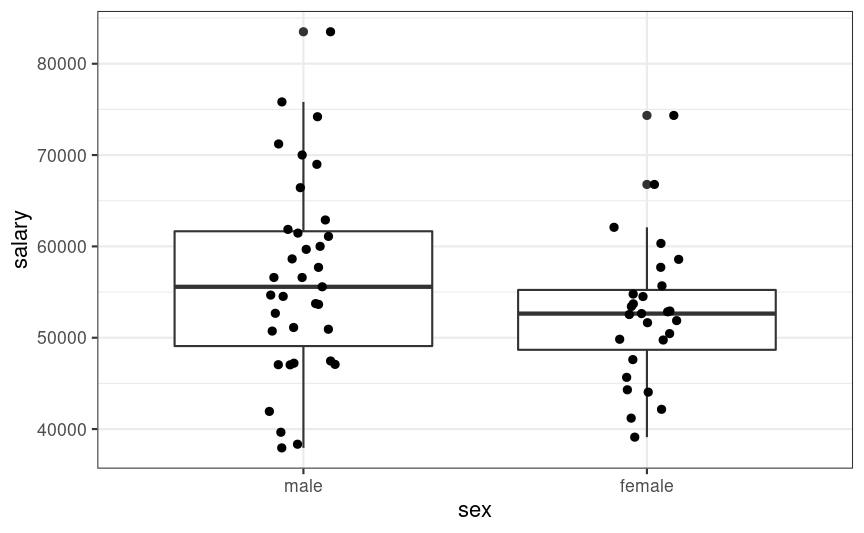
How does the distribution of
salarylook?Are there more males or females in the data?
How would you describe the relationship between number of publications and salary?
Explain what the x axis, y axis, diagonals are
Citation vs salary as an example
Simple Linear Regression
Sample regression line
Confidence intervals
Centering
- Regression line is only a sample estimate; there is uncertainty
- Uncertainty measured by standard errors and confidence intervals
- Show animations on the varying regression slopes
- A function of sample size
- Centering: Draw a picture on changing the x-axis
- Interpretations: unit increase in x associated with β unit increase in y
Categorical Predictors
Dummy Coding
With k categories, one needs k−1 dummy variables
The coefficients are differences relative to the reference group
Categorical Predictors
Dummy Coding
With k categories, one needs k−1 dummy variables
The coefficients are differences relative to the reference group
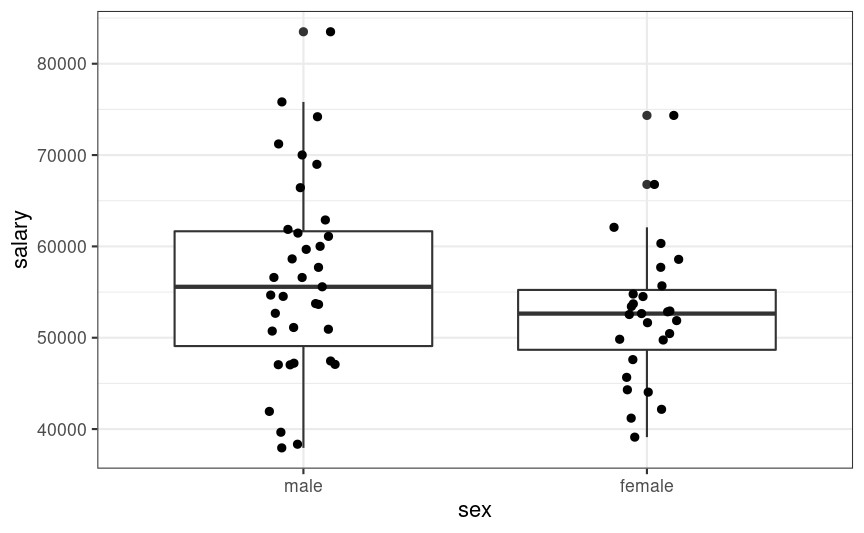
Categorical Predictors
Dummy Coding
With k categories, one needs k−1 dummy variables
The coefficients are differences relative to the reference group
Male = 0
y=β0+β1(0)=β0
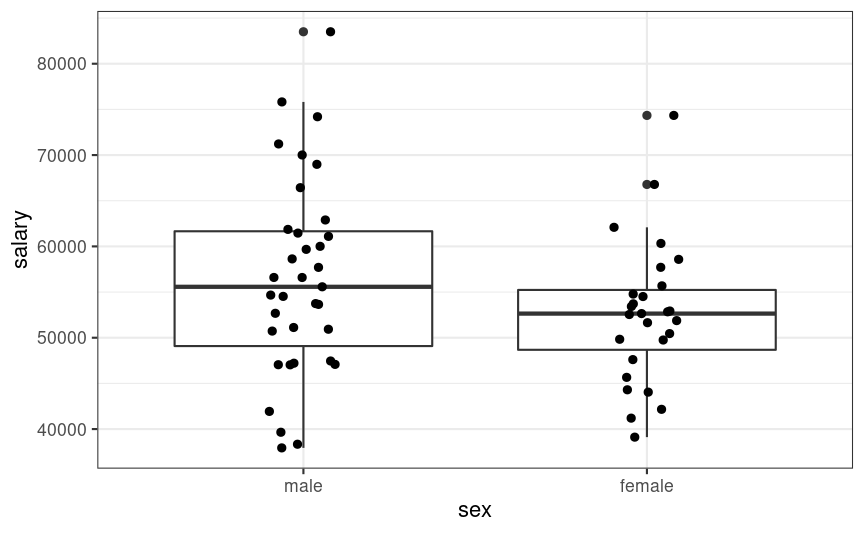
Categorical Predictors
Dummy Coding
With k categories, one needs k−1 dummy variables
The coefficients are differences relative to the reference group
Male = 0
y=β0+β1(0)=β0
Female = 1
y=β0+β1(1)=β0+β1
Multiple Regression
Partial Effects
salaryi=β0+β1pubci+β2timei+ei

Transition to R
Partial Effects
salaryi=β0+β1pubci+β2timei+ei

Interpretations
Every unit increase in X is associated with β1 unit increase in Y, when all other predictors are constant
Transition to R
Interactions
Regression slope of a predictor depends on another predictor
ˆsalary=54238+105×pubc+964×timec+15(pubc)(timec)
Interactions
Regression slope of a predictor depends on another predictor
ˆsalary=54238+105×pubc+964×timec+15(pubc)(timec)
time = 7 ⇒ time_c = 0.21
ˆsalary=54238+105×pubc+964(0.21)+15(pubc)(0.21)=54440+120×pubc
Interactions
Regression slope of a predictor depends on another predictor
ˆsalary=54238+105×pubc+964×timec+15(pubc)(timec)
time = 7 ⇒ time_c = 0.21
ˆsalary=54238+105×pubc+964(0.21)+15(pubc)(0.21)=54440+120×pubc
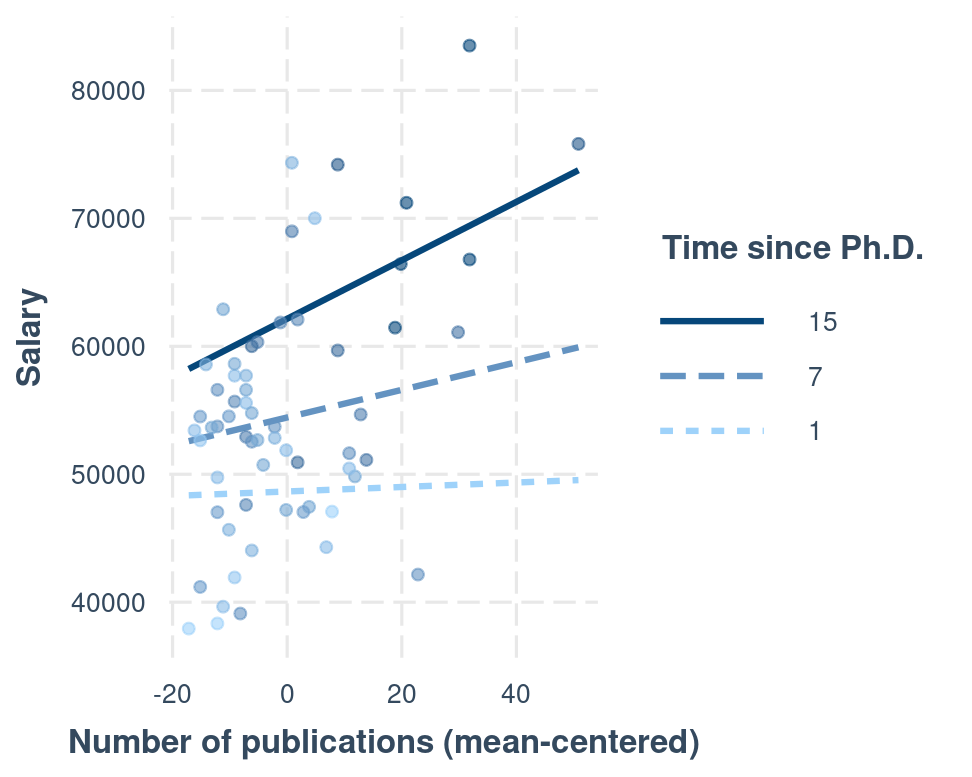
time = 15 ⇒ time_c = 8.21
ˆsalary=54238+105×pubc+964(8.21)+15(pubc)(8.21)=62152+228×pubc
Interactions
Regression slope of a predictor depends on another predictor
ˆsalary=54238+105×pubc+964×timec+15(pubc)(timec)
time = 7 ⇒ time_c = 0.21
ˆsalary=54238+105×pubc+964(0.21)+15(pubc)(0.21)=54440+120×pubc
time = 15 ⇒ time_c = 8.21
ˆsalary=54238+105×pubc+964(8.21)+15(pubc)(8.21)=62152+228×pubc
modelsummary::msummary()
| M3 + Interaction | |
|---|---|
| (Intercept) | 54238.1 |
| (1183.0) | |
| pub_c | 104.7 |
| (98.4) | |
| time_c | 964.2 |
| (339.7) | |
| pub_c × time_c | 15.1 |
| (17.3) | |
| Num.Obs. | 62 |
| R2 | 0.399 |
| R2 Adj. | 0.368 |
| AIC | 1291.8 |
| BIC | 1302.4 |
| Log.Lik. | −640.895 |
| F | 12.817 |
| RMSE | 7465.67 |
Summary
Concepts
What is a statistical model
Linear/Multiple Regression
Centering
Categorical predictor
Interpretations
Interactions